
Try to solve the maze. You can print it first.

Check back to see how a barrier method helped me solve it.
By the way, I got the second picture by using the command Sharpen[ ] in Mathematica software.
One week later: This is my solutionLong time ago, when I first tried to solve this maze, I kept getting tangled up in loops and couldn't solve it. Then I remembered something from my friend's research on Barrier Certificates. It seems like common sense, actually - to prove that there is no possible path, you show that there is a wall/barrier.
I thought to myself, "what if this maze can't be solved?" So I tried to find a wall across the maze. (If I had found one, then that would have been proof of a bad "unsolvable" maze.) I couldn't find a complete wall, but I found a broken wall.
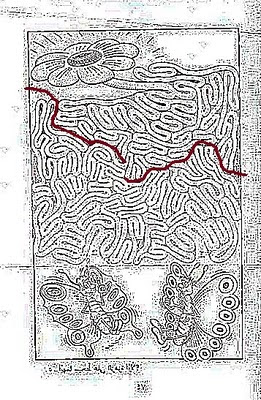
The broken wall is a great help in solving the maze. We know there is no path through the wall; if there's any path from butterfly to flower, then it passes through the crack in the wall. So search backwards from the crack to the flower and from the crack to the butterflies. Like this:

Here are some more mazes that you can solve more easily using barriers.











